En el cubo de Rubik original (3×3×3) tiene ocho vértices y doce aristas. Hay
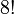 (40 320) formas de combinar los vértices del cubo. Siete de estas pueden orientarse independientemente, y la orientación de la octava dependerá de las siete anteriores, dando
(40 320) formas de combinar los vértices del cubo. Siete de estas pueden orientarse independientemente, y la orientación de la octava dependerá de las siete anteriores, dando 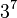 (2 187) posibilidades. A su vez, hay
(2 187) posibilidades. A su vez, hay 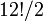 (239 500 800) formas de disponer los vértices, dado que una paridad de las esquinas implica asimismo una paridad de las aristas. Once aristas pueden ser volteadas independientemente, y la rotación de la duodécima dependerá de las anteriores, dando
(239 500 800) formas de disponer los vértices, dado que una paridad de las esquinas implica asimismo una paridad de las aristas. Once aristas pueden ser volteadas independientemente, y la rotación de la duodécima dependerá de las anteriores, dando  (2 048) posibilidades. En total el número de permutaciones posibles en el Cubo de Rubik es de:
(2 048) posibilidades. En total el número de permutaciones posibles en el Cubo de Rubik es de:
= 43 252 003 274 489 856 000
Es decir, cuarenta y tres trillones doscientos cincuenta y dos mil tres billones doscientos setenta y cuatro mil cuatrocientos ochenta y nueve millones ochocientas cincuenta y seis mil permutaciones.El rompecabezas es a menudo promocionado teniendo solo "millardos" de posiciones, ya que números más grandes no son muy familiares para la mayoría de la gente.CARAS CENTRALES
El cubo de Rubik original no tenía marcas en las caras centrales (aunque algunos traían las palabras "cubo de Rubik" en el cuadrado central de la cara blanca), y por ende resolverlo no requería prestar atención en orientar correctamente dichas caras centrales. Sin embargo, algunos cubos han sido producidos comercialmente con marcas en todos los centros, como el cuboku. Teóricamente puede resolverse un cubo aun teniendo los centros rotados; pero se convierte en un desafío adicional resolver también los centros.
Marcar los centros del cubo de Rubik aumenta su dificultad debido a que expande el conjunto de posibles configuraciones distinguibles. Hay 46/2 (2 048) maneras de orientar los centros, dado que una paridad de los vértices implica un número par de movimientos simples de los centros.
En particular, cuando el cubo es resuelto, aparte de las orientaciones de las caras centrales, siempre existirá un número par de caras centrales que requieren un giro de 90º. Dichas orientaciones de los centros incrementan el número total de permutaciones posibles del cubo de 43 252 003 274 489 856 000 (4.3×1019) a 88 580 102 706 155 225 088 000 (8.9×1022).21
Cuando girar un cubo alrededor de su propio eje es considerado como un cambio de la permutación, también es necesario contar las posibles posiciones de las caras centrales. En teoría, existen 6! formas de disponer las seis caras centrales del cubo, pero solo 24 de estas son posibles sin tener que desarmar el cubo. Cuando las orientaciones de los centros también son contadas, el total de las permutaciones incrementa de 88,580,102,706,155,225,088,000 (8.9×1022) a 2,125,922,464,947,725,402,112,000 (2.1×1024).
En la terminología de los aficionados al cubo de Rubik, una secuencia memorizada de movimientos que tiene un efecto deseado en el cubo es llamado algoritmo. Esta terminología deriva del uso matemático de algoritmo, un conjunto preescrito de instrucciones o reglas bien definidas, ordenadas y finitas que permite realizar una actividad mediante pasos sucesivos. Cada método de resolver el cubo emplea su propio conjunto de algoritmos, junto a descripciones de cuál es el efecto del algoritmo, y cuándo puede ser usado para llevar al cubo a un estado más cercano a estar resuelto.
Muchos algoritmos son diseñados para transformar solo una pequeña parte del cubo sin desarmar otras partes ya resueltas, y así poder ser aplicados repetidamente a diferentes partes del cubo hasta que quede resuelto. Por ejemplo, hay algoritmos para intercambiar tres vértices o cambiar la orientación de dos vértices sin cambiar al resto del rompecabezas.
Algunos algoritmos tienen un efecto deseado en el cubo (por ejemplo, intercambiar dos vértices) pero pueden tener efectos colaterales (como permutar dos aristas). Dichos algoritmos son a menudo más simples que otros sin efectos no deseados, y son empleados al principio de la solución cuando la mayor parte del rompecabezas no ha sido resuelto y los efectos secundarios no son importantes. Hacia el final de la solución son usados algoritmos más específicos (y por lo general más complejos) para evitar mezclar partes del cubo que ya han sido resueltas.
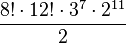
No hay comentarios:
Publicar un comentario